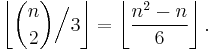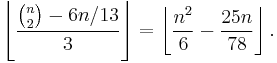Orchard-planting problem
In discrete geometry, the original orchard-planting problem asks for the maximum number of 3-point lines attainable by a configuration of points in the plane. Also called the Tree-planting problem, there are investigations into how many 4-, 5- & 6-point lines can be made. A variation is to restrict the plane to a square format such as a chessboard.
Contents |
Integer sequence
Define t3orchard(n) to be the maximum number of 3-point lines attainable with a configuration of n points. For an arbitrary number of points, n, the exact value of t3orchard(n) is generally not known. However, its value is known to be asymptotic to (1/6)n2.
The first few values of t3orchard(n) are given in the following table (sequence A003035 in OEIS).
| n | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| t3orchard(n) | 1 | 2 | 4 | 6 | 7 | 10 | 12 | 16 | 19 | 22 | 26 |
Upper and lower bounds
Since no two lines may share two distinct points, a trivial upper-bound for the number of 3-point lines determined by n points is
Using the fact that the number of 2-point lines is at least 6n/13 (Csima & Sawyer 1993), this upper bound can be lowered to
Lower bounds for t3orchard(n) are given by constructions for sets of points with many 3-point lines. The earliest quadratic lower bound of ~(1/8)n2 was given by Sylvester. This was improved to ~(1/6)n2 more recently by Burr, Grünbaum, and Sloane (1974). The best construction known is that of Füredi & Palásti (1984) which achieves ⌊(1/6)n2 − (1/2)n + 1⌋.
References
- Brass, P.; Moser, W. O. J.; Pach, J. (2005), Research Problems in Discrete Geometry, Springer-Verlag, ISBN 0387238158.
- Burr, S. A.; Grünbaum, B.; Sloane, N. J. A. (1974), "The Orchard problem", Geometriae Dedicata 2 (4): 397–424, doi:10.1007/BF00147569.
- Csima, J.; Sawyer, E. (1993), "There exist 6n/13 ordinary points", Discrete & Computational Geometry 9: 187–202, doi:10.1007/BF02189318.
- Füredi, Z.; Palásti, I. (1984), "Arrangements of lines with a large number of triangles", Proceedings of the American Mathematical Society 92 (4): 561–566, JSTOR 2045427.